*** KERGUELEN ***

Réponse… Enigme 180 – La mesure impossible serait-elle la meilleure…

     La presque totalité des élèves, ont mesuré au sol et en ligne droite depuis le premier point du mur d’entrée jusqu’au second du mur du fond. Là, ils annoncent fièrement la longueur mesurée au décamètre, soit 40 mètres. Ce calcul se faisant de tête très facilement aussi !

Le professeur les écoute attentivement sans rien dire. Il ne reste qu’un seul élève qui lui reste penché sur cette figure, perplexe. Le professeur se tourne alors vers lui en lui demandant.. ;

«  Eh bien mon ami, vous ne faites pas la mesure ? »

Et l’élève de répondre…

« Mais la mesure la plus courte est impossible à mesurer Monsieur. Il faudrait la dessiner sur un plan projeté des côtés et du plafond, et non pas mésuré sur le sol. C’est une figure impossible à mesurer à la main ».

Et là l’élève lui dessine le plan suivant… :

Surfaces projetées et développées en plan, de la salle de squash.

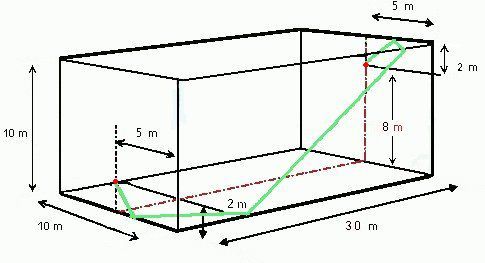
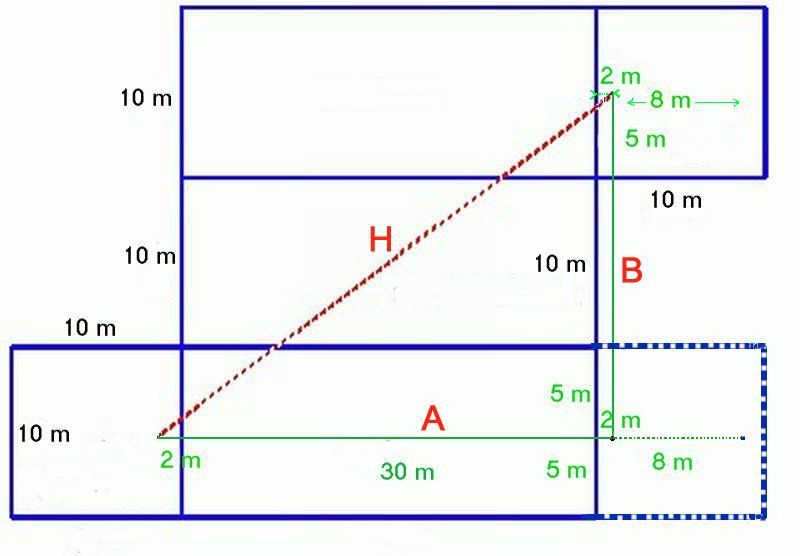
Et là, surprise ! Quand on fait ce calcul sur un tel plan développé, on s’aperçoit que la distance "H" est alors plus courte que celle mesurée en ligne droite, de tous les autres élèves.

En fait tout le monde a fait une erreur classique, c’est de prendre pour une mesure plane ce qui est un volume spatial à développer comme tel. Et quand on déroule un volume parallélépipédique à plat on obtient la figure dessinée suivant le plan développé, (figure plane en bleu).

En d’autres termes, le plafond ne se retrouve pas dans l’alignement du sol (bleu pointillé) mais décalé de 2 surfaces (vers la droite où vers la gauche, ce serait idem), celle du sol et d’un autre côté. La mesure en ligne droite sur le sol est donc une interprétation hâtive d’un volume. Dans ce cas la mesure de distance ne donnera donc pas la plus courte distance entre les deux points.

Notre dernier élève perplexe avait raison…

Seul le calcul mathématique permet de vérifier cette particularité.

Ainsi la mesure en ligne droite (qui est erronée) donne :

2 + 30 + 8 = 40 m entre les deux points rouges.

Sur la figure développée, il faudra alors prendre le triangle rectangle obtenu et calculer son hypoténuse.

« La longueur de l’hypoténuse d’un triangle rectangle égale la racine carrée de la somme des carrés des 2 autres côtés ». C’est le fameux théorème de Pythagore.

H² = A² + B² d’où H = R(A² + B²)… (où R= Racine de...).

Si on applique la formule au triangle rectangle obtenu, cela donne… :

A = 2 + 30 + 2 = 34 pour le premier côté

B = 5 + 10 + 5 = 20 pour le second côté

On aura donc…

H² = (34)² + (20)² = 1156 + 400 = 1556

D’où H = R(1556) = 39,45 m (R = Racine de)

Conclusion, la mesure la plus courte entre les deux points rouges, dessinée sur les murs d’entrée et du fond de la salle de squash, passe bien par le bout, puis le sol, puis le côté, encore le plafond, enfin le fond arrière en suivant une ligne brisée complexe. Elle ne sera pas facile à dessiner sur les parois, c'est certain.

Le dernier élève, encore perplexe, avait bien raison.

Mais en attendant, cette ligne brisée, cette « mesure impossible », sera bien la ligne la plus courte entre ces deux points repérés sur les murs de la salle de squash.

Voir ci-dessus la figure obtenue pour cette salle de squash, dans ce volume parallélépipédique.

Encore une fois, c'est toute la différence entre une chose "relative" et la même chose mais vu "dans l'absolu".

Une très belle citation d’Einstein pour illustrer cette énigme…

"La théorie c'est quand on sait tout et que rien ne fonctionne, la pratique c'est quand tout fonctionne et que personne ne sait pourquoi."

Retourner au site principal - page jeux et énigmes...